一般相対性理論は、「アインシュタイン」の名とともに広く知られる理論である。
次のアインシュタイン方程式で表される:
 この式は物質の分布が時空を曲げる関係を示す。左辺は時空の曲がりを、右辺は物質の分布を表す。理解にはリーマン幾何学、より正確には時空に拡張した「擬リーマン幾何学」の知識が必要となる。アインシュタインの提唱から100年以上を経た今も、新たな発見が続く理論である。
この式は物質の分布が時空を曲げる関係を示す。左辺は時空の曲がりを、右辺は物質の分布を表す。理解にはリーマン幾何学、より正確には時空に拡張した「擬リーマン幾何学」の知識が必要となる。アインシュタインの提唱から100年以上を経た今も、新たな発見が続く理論である。
理学の魅力を伝える
名古屋大学理学部・大学院理学研究科
Frontrunners
泉 圭介

一般相対性理論は、「アインシュタイン」の名とともに広く知られる理論である。
次のアインシュタイン方程式で表される:
 この式は物質の分布が時空を曲げる関係を示す。左辺は時空の曲がりを、右辺は物質の分布を表す。理解にはリーマン幾何学、より正確には時空に拡張した「擬リーマン幾何学」の知識が必要となる。アインシュタインの提唱から100年以上を経た今も、新たな発見が続く理論である。
この式は物質の分布が時空を曲げる関係を示す。左辺は時空の曲がりを、右辺は物質の分布を表す。理解にはリーマン幾何学、より正確には時空に拡張した「擬リーマン幾何学」の知識が必要となる。アインシュタインの提唱から100年以上を経た今も、新たな発見が続く理論である。
力の理解には「場」という概念が欠かせない。重力や磁力は、それぞれ重力場・磁場として空間に広がる。重力場に進む前に、電場を復習しよう。電場とは、空間の点に電荷を置いたとき、その電荷が受ける力を表す「場」である。電気力線は正電荷から出て負電荷に入る線であり、その密度が電場の強さを表す。
電場の基本法則の一つがガウスの法則である。これは「領域を囲む面を通る電場の強さから、その中の電荷量がわかる」という関係である。閉じた面内に電荷がなければ、出入りする電気力線は釣り合い、合計はゼロになる(図1)。逆に電荷があれば、その分だけ電気力線が出入りする(図2)。物体の電荷は内部を直接見ずとも、外側の電場から求められる点が重要である。さらに、電場には重ね合わせの原理が成り立つ。複数の電荷が作る電場は、それぞれの電場を足し合わせればよい。
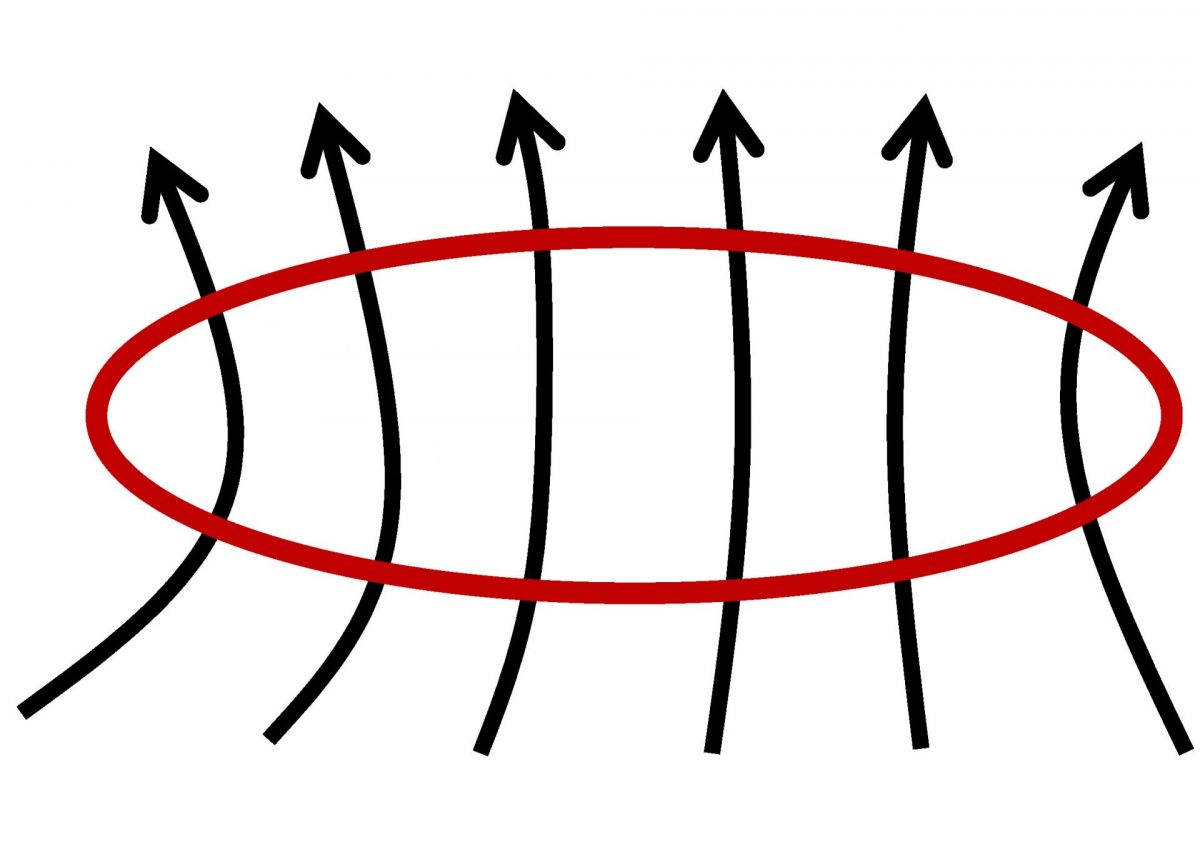
図1 電気力線のイメージ
黒色の矢印は電気力線(電場)を表している。赤で囲まれた領域に入る電気力線の本数と、出ていく電気力線の本数は等しい。
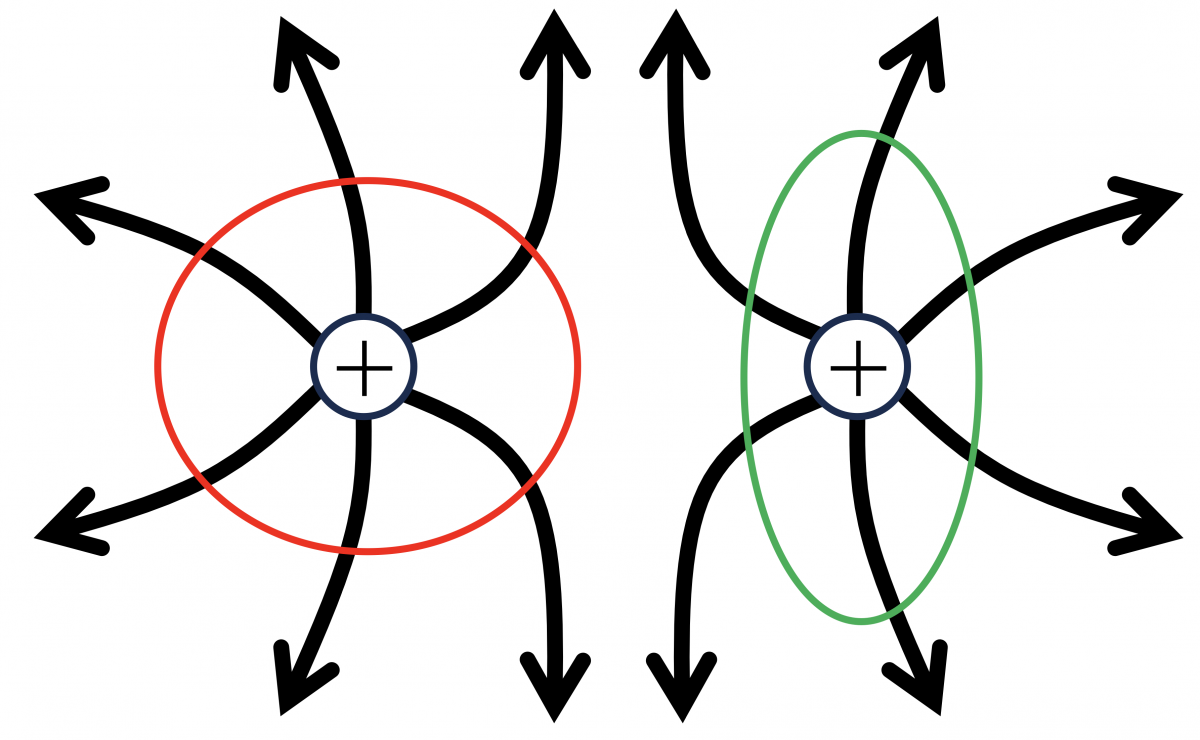
図2 2つの正電荷がつくる電場
2つの正電荷がつくる電場。電場は矢印で示している。左の電荷を知りたいときは、赤い面を通る電場の大きさの総和を調べればよい。右の電荷についても同様に、緑の面を通る電場の大きさの総和から求められる。囲む面の形は自由に選ぶことができる。
次に「重力場」を考えよう。日常の重力はニュートンの万有引力で説明されるが、それは「弱い重力場」の近似にすぎない。より正確には、アインシュタインの一般相対性理論が支配する。
アインシュタイン方程式(1)は非線形であり、「重ね合わせの原理」が成り立たない。複数の物体が作り出す重力場は単純に足せず、また、重力場自体もエネルギーを持つ。エネルギーと質量の等価性を表す式$\ E=mc^2\ $により、重力場のエネルギーも重力を生み出すため、重力場どうしが影響し合う複雑な関係が生じる。その結果、一般相対性理論では質量やエネルギーを厳密に定義することが難しくなる。
1979~81年、シェーンとヤウ[1,2]、そしてウィッテン[3]によって正エネルギー定理が証明された。この定理は、物質のエネルギーが正であれば、重力を含めた全体のエネルギーも正になることを意味している。
一般相対性理論は、ブラックホールという特別な時空領域の存在を予言している。ブラックホールとは「一度入ると二度と出られない」領域で、光さえ脱出できないため黒く見える。ここでは重力が非常に強く、ニュートンの理論では説明できない。この領域ではアインシュタイン方程式の非線形性が特に強く現れ、内部の「質量」を正確に定めるのは難しい。
それでも、ブラックホールの重力のもとになる質量は確かに存在する。その定め方の一つが、アインシュタイン方程式を満たすいくつかの時空の中から、遠くでニュートンの重力に近い振る舞いをするものを考え、その中で最も小さな「ADM質量」と呼ばれる値を取るものを選ぶ方法である。ペンローズは、この質量$m$とブラックホールの表面積$A$の間の関係を次のように予想した[4]:

これはペンローズ不等式と呼ばれ、ブラックホールの表面積から質量のおおよその下限を示す式である(図3)。この関係は、電場のガウスの法則のように「形から中身を推測できる」という点でよく似ている。ある特殊な状況下では証明が与えられている[5,6]。
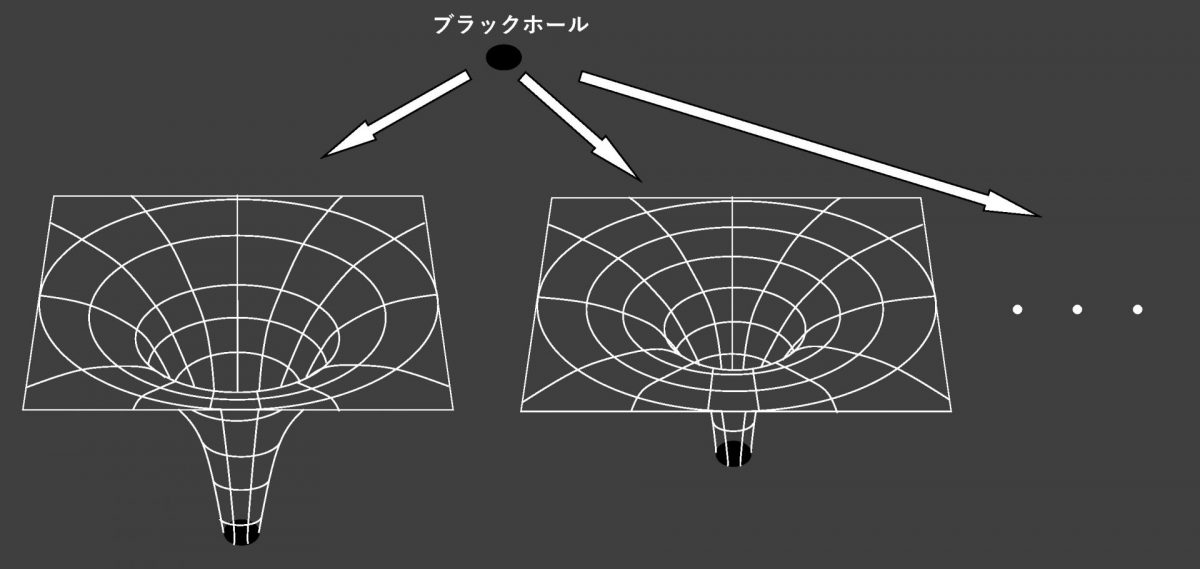
図3 ペンローズ不等式
あるブラックホールが存在すると仮定する(図上部)。このとき、その外側にはアインシュタイン方程式を満たす複数の時空解が存在しうる(図下部)。各解において、無限遠近傍ではADM質量が定義される。これらの解のうち、ADM質量が最小となるものを選び、そのADM質量を $m$ とする。このとき、$m$ とブラックホールの表面積 $A$ の間には、不等式(2)が成り立つという主張が、ペンローズ不等式である。
我々はペンローズ不等式の考え方を広げ、ブラックホール表面から遠く離れた領域までのあいだで選んだ面についても、特定の条件のもとで、面積と質量の間に似た不等式が成り立つことを示した[7,8,9]。これは中くらいの強さの重力場にも使える結果であり、ブラックホールが存在しない状況でも当てはまる。また、面を自由に選べるという点が、電場のガウスの法則と似ている点として興味深い。
このような「質量と面積の関係」を探る研究は、時空の幾何学的な性質を理解するうえで欠かせない。さらに、まだ完成していない「重力の量子化」への手がかりとしても重要である。ブラックホールや宇宙の始まりのような、重力が主役となる現象の研究は、今も発展し続けている。

数理学科 大学院多元数理科学研究科多元数理科学専攻准教授
1981年、岐阜県岐阜市に生まれる。2歳のときに大阪へ転居し、幼少期を大阪で過ごす。2004年、京都大学理学部を卒業。2009年、京都大学大学院理学研究科博士課程を修了。その後、東京大学数物連携宇宙研究機構、京都大学基礎物理学研究所、台湾大学Leung Center for Cosmology and Particle Astrophysics、バルセロナ大学理学部物理学科にて研究員を務める。2016年に本学に着任。本学では、基礎理論研究センター助教、素粒子宇宙起源研究所の助教・講師を経て、現在は名古屋大学大学院多元数理科学研究科准教授を務めている。専門は重力理論。一般相対性理論に加え、宇宙論や量子重力理論の研究も行っている。