「うまく数える」こと

子どもの頃、そろばん教室に通っていて、指慣らしとして1から100までの足し算をよくやっていた。何百回とやっていたため、答が5050であることは暗記していたのであるが、後に算数教室で

\begin{align*}
&(1 + 2 + \cdots + 100) + (100 + 99 + \cdots + 1) \\
&= (1 + 100) + (2 + 99) + \cdots + (100 + 1) \\
&= 100 \cdot 101
\end{align*}

から簡単に計算できることを知り、とても感動した記憶がある。今思うと、小学生の頃のこういった「うまく数える」という体験が、数学者を目指す原体験となっているように思う。子どもの頃に抱いた「うまく数える」ことへの憧れを、今でもなんとなく抱えている。

私の専門は代数幾何学という分野で、多項式の解集合として現れる図形を扱う幾何学である。実のところ、この分野では、このように「何かをうまく数える」タイプの問題はあまり見られない。しかし、専門とは別に行った研究で、まさにそのような問題に出会ったので紹介したい。

グラフとは、頂点とよばれる点の集合と、それを結ぶ辺の集合からなる対象である。その中でも周期グラフとは、次元と同じ数の並進対称性（平行移動で重なる性質）をもつようなグラフのことである。$2$次元の周期グラフは周期性をもつタイリングに自然に現れる（図1）。$3$次元の周期グラフは結晶の分子構造として自然に現れる（図2）。

図1　snub-$632$ 三様タイリング（左）と$3^2.4.3.4$ 一様タイリング（右）。図は論文［1］より引用。

図2　炭素同素体lonの結晶構造（左）と炭素同素体gsiの結晶構造（右）。結晶構造のデータは文献［4］の#37と#20からダウンロードした。 また図の描画にはVESTA（文献［5］） を利用している。

周期グラフの頂点を$1$つ固定し、その点から$n$ステップの移動で初めて到達可能な頂点の個数を$s(n)$と書くことにする。これにより得られる数列$(s(n))_n$は増大数列（growth sequence）とよばれている。

結晶学の文脈では、増大数列は配位数列（coordination sequence）とよばれている。この名前には、高校の化学で習う「配位数」の“数列バージョン”という意味が込められている（配位数は、隣接する原子の数のことであり、$s(1)$に他ならない）。例えば、$2$つの炭素同素体lon（図2左）とgsi（図2右）の配位数列は表1のようになる。図から結晶構造を区別するのが難しいときも、このように配位数列から区別可能なケースがある。

表1　lonとgsiの配位数列。

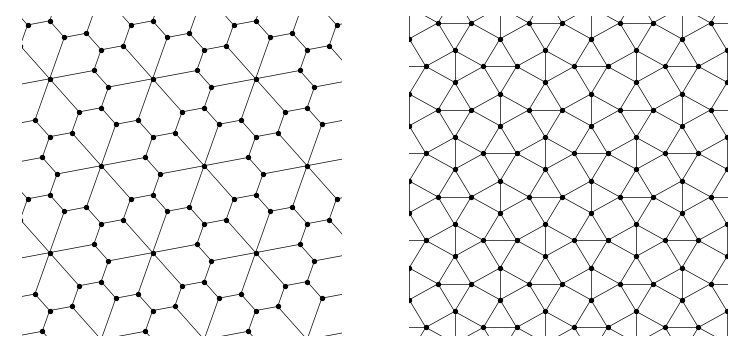
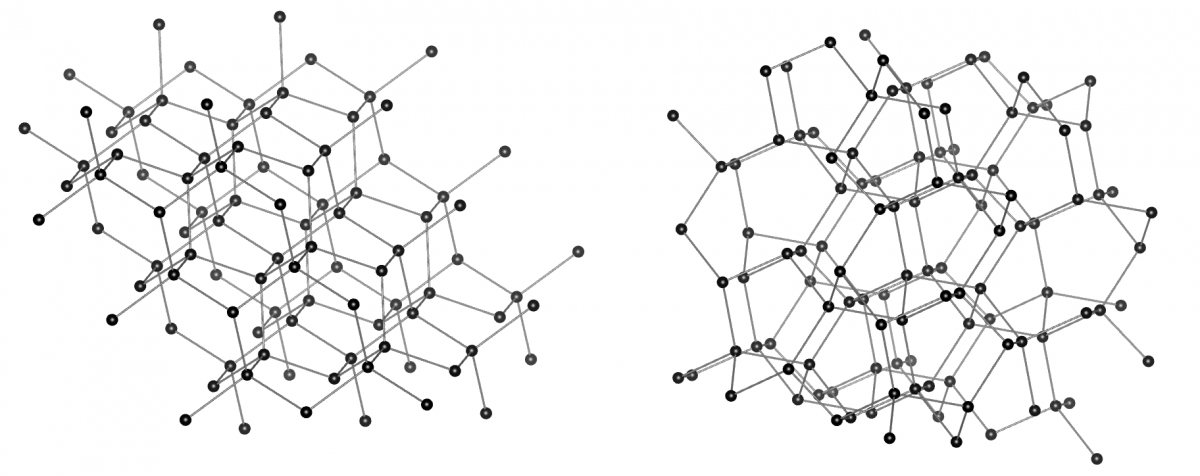
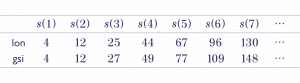数学の問題としては増大数列の一般項が気になる。gsiの配位数列の一般項は、$n \ge 4$において

\[
s(n)=
\begin{cases}
3n^2 + 1 & (n \equiv 0, 1 \mod 3) \\
3n^2 + 2 & (n \equiv 2 \mod 3)
\end{cases}
\]

で与えられる（$n=2,3$は例外項）。このように、有限項の例外を除き、周期的な多項式で表されるような関数を準多項式型の関数とよぶ。
一般的に次のことを論文［3］で証明した。

定理.　周期グラフの増大数列は準多項式型になる。

この事実自体は、1996年に論文［2］で予想されていたものである。この定理の証明には、群や環といった代数学の知識が使われている。元の問題と一見関係のないように思える代数学を利用して「うまく数える」ことができた点を非常に気に入っている。

代数学が証明にどのように登場するかを簡単に説明したい。具体的な$1$次元の周期グラフで考えてみよう。整数全体を頂点とし、各頂点からは$\pm 3$の方向と$\pm 5$の方向に計$4$本の辺が出ているような周期グラフを考える。この場合、増大数列$s(d)$は「$-5, -3, 3, 5$を使った$d$個の足し算で書くことのできる数であって、$d-1$個以下の足し算で書くことができないもの」の個数に他ならない。これを「代数学的に数える」方法を説明したい。まず、$4$つの数$-5, -3, 3, 5$に対応して、（第$1$成分に$1$を追加して得られる）$4$つのベクトル$(1, -5), (1, -3), (1, 3), (1, 5)$を考えることがポイントとなる。これらに$(1,0)$を加えた$5$つのベクトルを使った有限個の和で書けるようなベクトル全体を$B$と表すことにする。また、正の整数$d$に対し、$B$の元であって第$1$成分が$d$となるもの全体を$B_d$で表し、$b(d)$で$B_d$の元の個数を表すことにする。$B_d$や$b(d)$は何を表しているだろうか。少しややこしいかもしれないが、$B_d$の第$2$成分に、「$-5, -3, 3, 5$を使った$d$個以下の足し算で書くことのできる数」がすべて現れることが分かると思う。従って、$b(d)$はそのような数の個数に他ならず、増大数列$s(d)$は$s(d) = b(d) – b(d-1)$と表すことができる。よって、$s(d)$が準多項式型であることを示すためには、$b(d)$が準多項式型であることを示せば十分である。ここまで来ると、代数学の一般論から証明を完結することができる。$B$のように、足し算の操作で閉じている集合はモノイドとよばれる代数学的な対象である。そして、$B_d$の元の数$b(d)$が準多項式型になることは、次のような代数学の一般論から証明できるのだ。

（参考）ヒルベルト級数の理論.　$n$を正の整数とする。${\bf a}_1, \ldots , {\bf a}_{\ell}$を$n+1$次元のベクトルとし、それらの第$1$成分はすべて正の整数であると仮定する。${\bf a}_1, \ldots , {\bf a}_{\ell}$を使った有限個の和で書けるようなベクトル全体を$B$と表す。また、正の整数$d$に対し、$B$の元であって第$1$成分が$d$となるもの全体を$B_d$で表し、$b(d)$で$B_d$の元の個数を表すことにする。このとき、$b(d)$は準多項式型となる。

$2$次元以上の周期グラフであっても、すべての頂点から同じ方向に辺が出ているケースでは、上の議論が同じように機能する。一般の周期グラフについては、頂点の種類によってそこから出ている辺の方向が異なることがあるため、$B$のようなモノイドが対応しない。そのため、組合せ論的なアイデアがもう一つ必要となる。

最後にこの分野の未解決問題を紹介して終わりにしたい。lonの配位数列の一般項は、$n \ge 1$において次の準多項式で与えられる。

\[
s(n)=
\begin{cases}
\frac{21}{8}n^2 + 2 & (n \equiv 0 \mod 4) \\[1mm]
\frac{21}{8}n^2 + \frac{11}{8} & (n \equiv 1, 3 \mod 4) \\[1mm]
\frac{21}{8}n^2 + \frac{3}{2} & (n \equiv 2 \mod 4)
\end{cases}
\]

このlonの配位数列$s(n)$は次の二つの点で特殊である。 

　$(1)$ 準多項式で表したときに例外項がない。
　$(2)$ 準多項式が$s(-n) = s(n)$をみたす。

一方で、gsiの配位数列は条件$(1)$をみたさないだけでなく、条件$(2)$もみたしていない。gsiに現れる準多項式は、

\[
s(-n)=
\begin{cases}
3n^2 + 1 & (n \equiv 0, {\bf 2} \mod 3) \\
3n^2 + 2 & (n \equiv {\bf 1} \mod 3)
\end{cases}
\]

となり元の$s(n)$に一致しない。

lonだけでなく、（対称性の高い）周期グラフの多くが条件$(1)$と$(2)$をみたすことが数理結晶学と組合せ論の双方の分野で報告されている。論文［1］において、「条件$(1)$と$(2)$が成立するための周期グラフの特徴付け」に取り組んだが完全には解決できていない。果たして、どういったグラフ理論的な条件（lonがみたしgsiがみたさない条件）がこの$2$条件を成り立たせているのだろうか。代数幾何学的な視点から見ると、この$2$条件は、コホモロジーの消滅定理や双対性といった幾何学的な条件に見えてくる。代数学に加えて、代数幾何学的な視点が有効かもしれない、と思いつつたまに考えている。